(Updated on 09/09/2015)
1. Waves are caused by oscillations or vibrations of particles of the medium in which the waves travel.
1. Waves are caused by oscillations or vibrations of particles of the medium in which the waves travel.
(An inquisitive student may ask: What about the travel of electromagnetic waves through vacuum, say, from the Sun to our Earth's atmosphere? Doesn't the aforesaid statement imply that there must be particles in oscillations in vacuum to transmit the electromagnetic waves? And that the particles must be mass-less and invisible since vacuum is mass-less and invisible? Are there such particles in vacuum? If you are one of these inquisitive students, I encourage you to probe these questions all the way to PhD level. If you can't find clear and convincing answers there, then do try to provide answers for us. For SPM, answer this question: Yr 2007, P1, Q34 without hesitation)
2.
An oscillation
(or vibration) is a movement of a particle or body back and forth along a
line about a fixed central position. An oscillation can be illustrated with a swinging pendulum or an oscillating loaded spring. (The fixed central position can also be referred to as the mean position or the equilibrium position).
3.
Waves transfer energy (and momentum, in a closed mechanical system) from
the oscillating source without transferring matter:
a.
When waves travel through a medium, the
particles of the medium merely vibrate or oscillate about their equilibrium positions
– the particles do not travel in the direction of the waves.
b.
Experimental proofs:
i.
The “radio
& candle flame” experiment - the candle flame swaying back
and forth and not pushed to one direction only; or
ii.
The “floating
ball" on water waves – the ball moves up and down on the same spot without
moving in the direction of waves.
4.
There are two types of waves, namely:
a. Transverse
waves where the vibrations of the particles are at right angle or perpendicular to the direction of
propagation of the waves - e.g. water waves (SPM Yr 2012 P1 Q34 @ pg 339 / 2012 P2 Q2 @ pg. 347) and electromagnetic waves including visible
light; or,
b.
Longitudinal
waves where the vibrations of the particles are parallel to the direction of propagation such as sound waves.
5.
Production of waves (of different types)
:
:
a.
Water
waves are produced by a disturbance
or a series of disturbances on a water surface causing oscillations of
water particles which produce the water waves.
b.
Sound
waves are produced by a disturbance
or a series of disturbances on air particles such as by hitting a tuning fork, plucking a guitar string, moving the diaphragm of a audio speaker by an electromagnetic mechanism, etc..
c.
Electromagnetic
waves (including light) are
produced by oscillations of electrons in an atom; or, movement of electron from a higher energy orbital to a lower energy orbital.
(Note: When you go to A-level, you will be more familiar with the concept of electron orbitals (s, p, d, f... orbitals rather than orbits for electrons) and the Heisenberg Uncertainty Principle as to the position and behaviour of electrons at any time. At O-level, it is okay to think of electrons as orbitting the atomic nuclues)
(Note: When you go to A-level, you will be more familiar with the concept of electron orbitals (s, p, d, f... orbitals rather than orbits for electrons) and the Heisenberg Uncertainty Principle as to the position and behaviour of electrons at any time. At O-level, it is okay to think of electrons as orbitting the atomic nuclues)
6.
A wavefront
is an imaginary line or plane that joins all the points or particles in a wave
which are in the same cycle and in the same phase of vibration – meaning, a line joining all the points or particles which are in the same cycle of the waves and in the same direction and magnitude of
displacement from the mean position of vibrations - for examples: the line that joins all the points
on the crests or all the points on the troughs of waves as shown below:


7. The direction
of propagation (or, travel) of a wave is always perpendicular to its wavefront.
8.
The amplitude,
a, of an oscillation is the maximum
displacement from the mean or equilibrium position of the oscillation:
a) Diagram showing the amplitude of a wave:
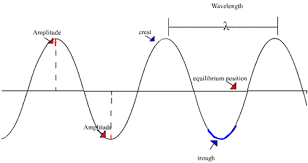
b) Diagram below shows three possible amplitudes of a swinging pendulum: Ө, x or H. (In experiments, Ө can be easily measured with a protractor; and, x and H can also be measured with metre rule; however, between x and H, x will give lower % of error since when x > H even if parallax or 'line of sight' error is avoided - On this, try IGCSE Physics 0625 Oct/Nov 2009 Paper 32, Question 1(b)):
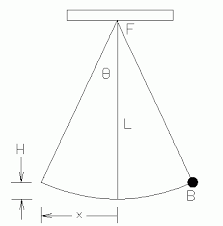
a) Diagram showing the amplitude of a wave:
b) Diagram below shows three possible amplitudes of a swinging pendulum: Ө, x or H. (In experiments, Ө can be easily measured with a protractor; and, x and H can also be measured with metre rule; however, between x and H, x will give lower % of error since when x > H even if parallax or 'line of sight' error is avoided - On this, try IGCSE Physics 0625 Oct/Nov 2009 Paper 32, Question 1(b)):
9.
The period,
T, of the oscillation is the time taken to complete one oscillation.
a.
A complete oscillation means a complete movement
of a vibrating point from a reference point in a direction along a path and back to the same reference point and moving in the same direction - for examples: a pendulum moving from one extreme position to the other and back to the
original extreme position; a loaded spring moving from the extreme bottom to the extreme top position and back to the extreme bottom.
b.
T = Tn /
N, where Tn = Time for n number of oscillations; and N = n number of
oscillations.
c. Relationship between T and f and vice versa: Period T
is inversely proportional to the frequency
f (T = 1/f) and the converse is also true - f is inversely proportional to T (f = 1/T).
d. Relationship between T and 1/f and f and 1/T: Period T is not "directly proportional" to 1/f because 1/f can never be zero - and, the straight line graph of T against 1/f never passes through the origin. The relationship is therefore: T increases linearly with 1/f; and, for the same reason, f increases linearly with 1/T.
d. Relationship between T and 1/f and f and 1/T: Period T is not "directly proportional" to 1/f because 1/f can never be zero - and, the straight line graph of T against 1/f never passes through the origin. The relationship is therefore: T increases linearly with 1/f; and, for the same reason, f increases linearly with 1/T.

10.
The frequency,
f, of a wave is the number of
oscillations made in one second.
a.
f = N /
Tn, where Tn = Time for n number of oscillations; N = n number of
oscillations; and Tn / N = T (see: 9 (b) above)
b.
Since Tn / N = T and f = N / Tn, therefore f =
1/T (Frequency f is inversely proportional to period T; or f increases linearly with 1/T) or T = 1/f (Period T is inversely propertional to frequency f; or, T increases linearly with 1/f) (Express
these as graphs of: f vs.T; f
vs.1/T and T vs.1/f;).
11.
The wavelength, λ:
a. The horizontal distance between 2 successive points of the waves which are in the same phase of oscillation or between 2 successive wavefronts – e.g.
between 2 successive crests or 2 successive troughs; or
b.
The distance travelled by waves in 1 complete oscillation / cycle.
12.
Wave speed,
v = distance travelled / time taken = wavelength / period ( v = λ/T)
or, v =
wavelength x frequency (v = λf)
[SPM 2012 P2 Q2(c) @ pg 348 asks:
When the frequency of the water wave is increased, what happens to:
(i) The wavelength of the water wave?
(ii) The speed of the water wave?
Answers:
(i) The wavelength decreases (since in the same medium - i.e. water of the same depth in the ripple tank - wave travels at the same speed and speed being v = λf means that when f increases, wavelength λ must decrease for wave speed v to remain the same).
(ii) The speed remains unchanged (since nothing is mentioned about the depth of the water in the ripple tank being altered. Q only mentions frequency f is increased)]

[SPM 2012 P2 Q2(c) @ pg 348 asks:
When the frequency of the water wave is increased, what happens to:
(i) The wavelength of the water wave?
(ii) The speed of the water wave?
Answers:
(i) The wavelength decreases (since in the same medium - i.e. water of the same depth in the ripple tank - wave travels at the same speed and speed being v = λf means that when f increases, wavelength λ must decrease for wave speed v to remain the same).
(ii) The speed remains unchanged (since nothing is mentioned about the depth of the water in the ripple tank being altered. Q only mentions frequency f is increased)]
13.
Displacement
vs. Time Graph of a Wave:


This graph shows the displacement of a vibrating loaded spring about its mean position against the time in graphical form. It is a sinusoidal graph from which we can obtain
This graph shows the displacement of a vibrating loaded spring about its mean position against the time in graphical form. It is a sinusoidal graph from which we can obtain
a.
the amplitude,
a; and
b.
the period
T; and thus,
c.
the frequency,
(by f = 1/T)
of the waves.
(For sound waves: the Displacement vs. Time graph can be replaced with Pressure vs. Time graph)
If we want to calculate the speed of the wave v, we need to know the wavelength λ (v = λf) - the wavelength λ is obtainable from another graph known as Displacement vs. Distance Graph.
(For sound waves: the Displacement vs. Time graph can be replaced with Pressure vs. Time graph)
If we want to calculate the speed of the wave v, we need to know the wavelength λ (v = λf) - the wavelength λ is obtainable from another graph known as Displacement vs. Distance Graph.
14.
Displacement
vs. Distance Graph of a Wave:

It shows the displacement of vibrating particles in a wave against their distances from the oscillating source in graphical form – The D vs. d graph is also a sinusoidal graph from which we can obtain

It shows the displacement of vibrating particles in a wave against their distances from the oscillating source in graphical form – The D vs. d graph is also a sinusoidal graph from which we can obtain
a.
the amplitude,
a; and
b.
the wavelength, λ;
of the waves. (Please see: SPM 2012 P1 Q31 @ pg 338).
If we want to calculate the speed of the wave, we need to know the frequency f or the period T, since v = λf; or v = λ/T; and we can obtain f from the earlier graph (D vs. time graph).
(For sound waves: the Displacement vs. Distance graph can be replaced with Pressure vs. Distance graph)
15.
The energy
carried by a wave depends on its amplitude (for mechanical waves like water waves, sound waves, etc) or frequency (for electromagnetic waves).
[For discussion: Please refer SPM Yr 2005, P1, Q35 (pg. 11):
Q35 gives 4 graphs which show the cross-sections of water waves. Q35 asks: Which wave has the greatest energy?
Wave C has higher amplitude and wave D has higher frequency (than waves A and B). So, should your answer be wave C or wave D; And, why? What would your answer be if the waves are electromagnetic waves instead of water waves?] Answer C (energy of water waves depends on amplitude)]
If we want to calculate the speed of the wave, we need to know the frequency f or the period T, since v = λf; or v = λ/T; and we can obtain f from the earlier graph (D vs. time graph).
(For sound waves: the Displacement vs. Distance graph can be replaced with Pressure vs. Distance graph)
[For discussion: Please refer SPM Yr 2005, P1, Q35 (pg. 11):
Q35 gives 4 graphs which show the cross-sections of water waves. Q35 asks: Which wave has the greatest energy?
Wave C has higher amplitude and wave D has higher frequency (than waves A and B). So, should your answer be wave C or wave D; And, why? What would your answer be if the waves are electromagnetic waves instead of water waves?] Answer C (energy of water waves depends on amplitude)]
16.
Natural
frequency:
a.
Anything that can oscillate if left to oscillate
freely will oscillate at its natural frequency.
b.
Natural
frequency is therefore the frequency at which an oscillating system will
oscillate without the action of any external force.
17.
Damping:
a.
A body oscillating freely at its natural
frequency but with decreasing amplitude is said to experience damping. Graphically, damping is shown as follows:
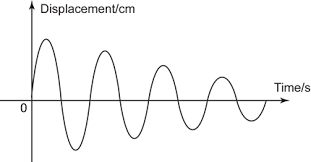
b.
Damping
occurs in an oscillating system when the system loses energy resulting in the
decrease in amplitude but not the frequency of the oscillation.
c.
Examples: A pendulum swinging freely or a loaded spring oscillating freely in a non-vacuum environment will see the amplitude
of its swing (or oscillation) gradually decreases (while the frequency remains
unchanged) until the swinging or oscillation stops:
d.
When damping occurs, energy is lost in two possible ways:
i.
To overcome frictional forces whether in air or in liquid – External damping;
ii.
Due to the extension or compression of the
vibrating particles – Internal damping.
e.
To overcome
damping, external force must be applied (thus energy is supplied) to keep
the amplitude from decreasing. Such an oscillation is called forced oscillation.
18.
Resonance:
a.
Resonance
occurs in an oscillating system when the system is driven or made to
oscillate at its natural frequency by an external periodic force.
b.
When resonance occurs, the system oscillates at
its maximum amplitude.
(For resonance in tuning forks: please see SPM 2012 P1 Q32 @ pg 338.)
c.
Examples of resonance:
ii.
Tuning
radio or television to the frequency of the station or the channel – when
tuner's frequency and the station's frequency are the same, resonance occurs to
cause increase in amplitude of the radio wave and therefore better reception
and clarity.
iii. Loudness and clarity of musical notes by wind-pipe
instruments such as saxophones, trumpet, flute and the likes: When some particular
keys or holes are pressed, the natural frequency of the wind pipe changes.
Frequency of air vibrations caused by blowing which matches the natural
frequency of the wind pipe causes resonance to occur resulting in loud and
clear musical notes.
iv. Tacoma Narrows Bridge disaster in USA
in 1940 – wind blowing at the natural frequency of the suspension bridge causing
it to resonate and vibrate with maximum amplitude resulting in its collapse.
------------------------------------------------------------
19. Crests and Troughs of Water Waves Act as Lenses (SPM 2012 P2 Q2 @ pg 347):
In ripple tank experiments, you will note that there is a lamp placed above the tank shining light down through the water waves creating on the white paper placed below the tank a water waves pattern consisting of bright bands (representing the crests) and darker bands (representing the trough) . This happens because:
- Crests act as convex lens - converging light - creating bright bands on the paper (SPM 2012 P2 Q2(b)(i) @ pg 347); whereas,
- Troughs act as concave lens - diverging light - creating darker bands. (SPM 2013?)
- This device enables us to view moving water waves as stationary waves.
- Water waves appear stationary when the water waves frequency, f is equal to the frequency of the stroboscope fs multiplied by the number of slits n on the stroboscope: f = n x fs


No comments:
Post a Comment